Investigando qué polígonos regulares pueden teselar el plano

La finalidad de esta práctica es descubrir con qué polígonos regulares puede recubrirse el plano y por qué.

Triángulos equiláteros

• Abrimos el programa Geogebra y quitamos los ejes de coordenadas y la cuadrícula.

• Seleccionamos, la herramienta [Polígono regular]:

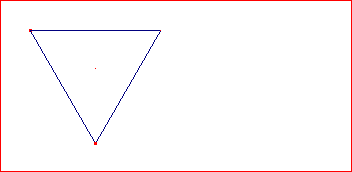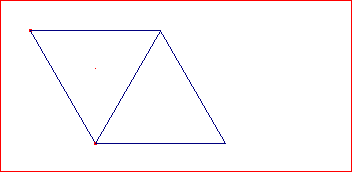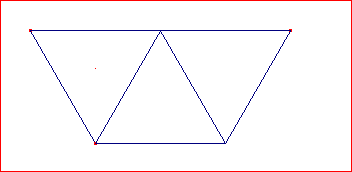
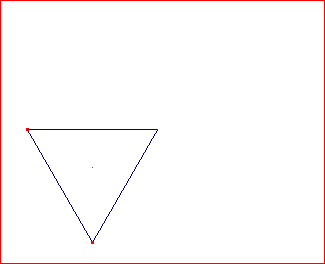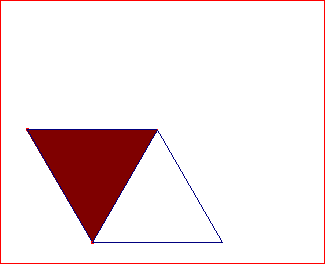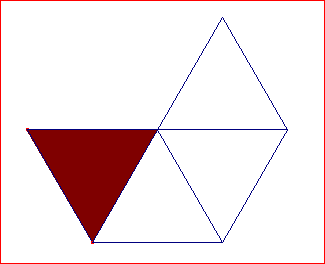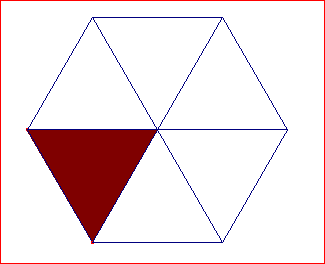
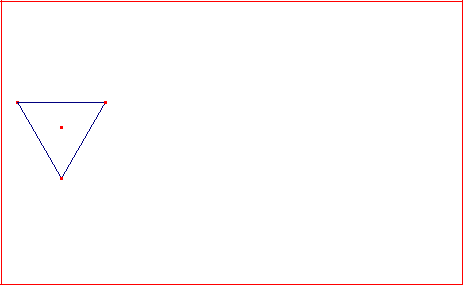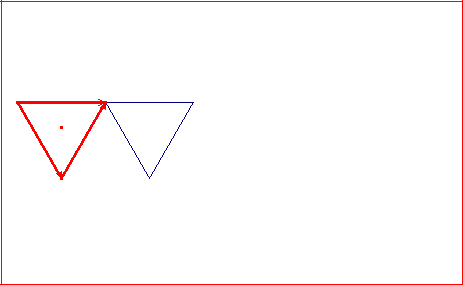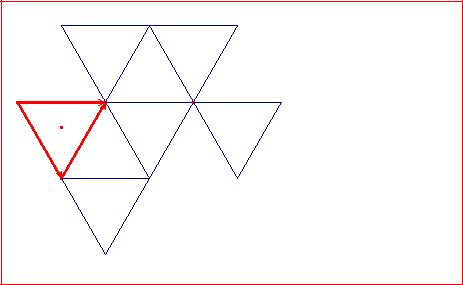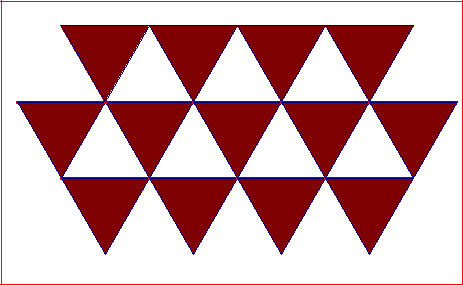
• Con el icono seleccionado hacemos clic con el botón izquierdo del ratón sobre dos puntos de la pantalla para fijar el lado del polígono y después y se nos pedirá e numero de lados (escribimos tres) y tenemos dibujado nuestro triángulo equilátero:

 Ahora hemos de comprobar si tesela el plano utilizando simetrías axiales (o mediante giros de 60º en torno a los vértices):

• Vamos a usar la herramienta [Refleja objeto en recta] para dibujar el simétrico al triángulo respecto de uno de sus lados.

• Repitiendo los pasos anteriores para el triángulo de la derecha obtenemos su simétrico:

• Continuamos dibujando tres triángulos más con el mismo procedimiento y comprobamos que recubren el plano formando un hexágono regular :

Podemos obtener al mismo resultado usando giros de 60º con la herramienta[Rota objeto en torno a punto]

Una vez que hemos comprobado que los triángulos equiláteros teselan el plano, en el mismo archivo vamos a dibujar el mosaico, pero ahora usando traslaciones, en vez de simetrías:

• En otro punto de la pantalla dibujamos otro triángulo equilátero que reflejamos, como hemos indicado anteriormente, usando como eje uno de sus lados.

• Seleccionamos la herramienta [Vector entre dos puntos] y dibujamos los tres vectores que forman sus lados seleccionando los puntos origen y extremo de los segmentos que forman la base (hacia la derecha) el lado derecho (hacia arriba) y el izquierdo (hacia abajo).

• Seleccionamos la herramienta [Traslada objeto vector], y seleccionamos el triángulo y lo trasladamos según lostres vectores dibujados en el punto anterior. Para rellenar "los huecos" usa el otro triángulo trasladándolo con los vectores del primero que necesites.

• Para continuar dibujando el mosaico sólo tienes que continuar el procedimiento en las direcciones que desees seleccionando los triángulos adecuados y el vector según el cual lo vas a trasladar, hasta formar un mosaico similar a :

• Guarda el archivo, seleccionando la opción correspondiente del menú < Archivo >  , con el nombre {Mosatri}.

• Mediante la herramienta[Texto]del penúltimo grupo escribid vuestros nombres y pedid permiso para imprimir el dibujo y entregarlo al profesor/a.

A continuación se muestran unos diseños basados en la teselción del plano mediante triángulos:

En este enlace trato los patrones basados en el triángulo de Pascal.

Cuadrados

Vamos a comprobar que se puede teselar el plano usando cuadrados:

• Abrimos un archivo nuevo (y cerramos el anterior).

• Dibujamos un cuadrado y, mediante la herramienta[Refleja objeto en recta], (también podemos usar giros de ¿cuántos grados?), vamos dibujando a su alrededor otros tres cuadrados hasta completar la teselación del plano.

• Prolonga el mosaico (¿cuántos vectores necesitas ahora?), escribe el nombre, guarda el archivo con el nombre {Mosacua}, pide permiso para imprimirlo y entrégalo.

A continuación se muestran unos diseños basados en la teselación del plano mediante cuadrados:

Con un poco de paciencia podemos conseguir mosaicos más reales y con imaginación más "artísticos":

Mi portal

Prueba si el pentágono regular, el hexágono, etc., teselan el plano

En esta pagina tienes un estudio con Geogebra y Flash de las isometrías de los polígonos regulares.

Para descubrir la propiedad que han de cumplir los polígonos regulares que forman mosaico, continua probando con el resto de los polígonos regulares, siguiendo el procedimiento anterior y rellena una tabla semajante a la del Apéndice A (escribe en el recuadro, cuando lo sepas, la condición que han de cumplir los polígonos regulares que teselan el plano) que has de entregar cuando termines junto con los mosaicos construidos.