La finalidad de esta práctica es la de profundizar en algunos principio geométricos, paralelismo, perpendicularidad, giros, traslaciones y simetrías al confeccionar los 8 mosaicos semirregulares.
Un mosaico es semirregular si para su construcción se utilizan dos o más tipos de polígonos regulares con sus vértices en contacto, repitiéndose la misma disposición geométrica de los polígonos en todos los vértices del mosaico.
Como la suma de los ángulos en cada vértice ha de ser de 360º, el número mínimo de polígonos regulares de igual lado que pueden concurrir en un vértice es de 3 y el número máximo de 6.
Teniendo en cuenta que el ángulo interior de un polígono regular de n lados bien dado por
![]() ,
en el vértice común habrá de cumplirse
:
,
en el vértice común habrá de cumplirse
:
si extraemos factor común en el primer miembro a 180º y lo pasamos al segundo dividiendo queda:
al sumar k veces 1 nos queda k y cambiando de signo y transponiendo tenemos finalmente :
Ahora sólo tenemos que ir dando k = 3,4,5 y 6 y obtener los valores de n >2 y natural que cumplen la igualdad. Encontramos 17 soluciones distintas, algunas de las cuales admiten dos formas distintas de ordenarlas, consiguiendo al final 21 modelos posibles de vértices, pero de esos 21 sólo 8 tiene polígonos regulares distintos y pueden repetirse indefinidamente.
Vamos a dibujar con el programa Geogebra, paso a paso, uno de esos ocho mosaicos semirregulares, el que concurren en un vértice 1 triángulo, 1cuadrado, 1 hexágono y otro cuadrado (3,4,6,4 según la nomenclatura de Schläfi) para ir conociendo algunas de las posibilidades del programa Geogebra. No partimos de la loseta básica ni seguimos el método formal pues la finalidad aquí es sólo una introducción a Geogebra al tiempo que presentamos los mosaicos semirregulares, veamos algunos:
- Utilizando la herramienta[Polígono Regular] dibujamos un hexágono regular marcando los dos puntos del lado e introduciendo 6 para el número de lados. Después seleccionamos el color, el estilo de línea y el sombreado deseado en su propiedades. En cada uno de los seis lados del hexágono levantamos un cuadrado de lado el del hexágono usando la misma herramienta pero eligiendo cuatro para el número de lados. Sólo has de tener cuidado de pulsar en los vértices del hexágono en sentido horario para que los cuadrados se dibujen en el exterior y no en el interior del hexágono.
- Para seguir ampliando el mosaico, dibujando los seis hexágonos del segundo nivel por los vértices de los seis cuadrados dibujados en el paso anterior.
- Seguimos ampliando el mosaico dibujando cuadrados alrededor de los hexágonos del segundo nivel:
Ten en cuenta que los triángulos formados no existen para Geogebra mientras no los dibujes con la herramienta [Polígono] si deseas rellenarlos de color.
- Escribe tu nombre, guarda el archivo con nombre {Semi3464} y pide permiso para imprimirlo.
El procedimiento es válido y puede seguirse hasta el infinto (o hasta dónde lo necesites) pero si has tenido la suficiente paciencia como para seguir todo el proceso habrás comprobado que es lento y repetitivo, ¿existe alternativa? La alternativa tampoco es sencilla por la incapacidad de Geogebra para agrupar varios objetos (esperemos que se implemente en futura esta posibilidad). Si partimos del dominio fundamental y aplicamos las isometrías características de este grupo isométrico podemos obtener la loseta básica que mediante traslaciones en las dos direcciones del plano nos proporcionrán el mosaico.
En la página que he confecionado sobre la loseta básica hemos visto que el motivo mínimo de este mosaico es:
Vamos a dibujarla y después aplicando las isometrías que correspondan ontendremos la celda o dominio fundamental.
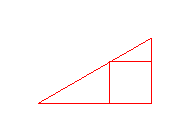
- Dibujamos un triángulo equilátero y trazamos sus mediatrices![]() (que también son alturas, bisectrices y medianas), cada uno de los seis triángulos rectángulos formados es la base para la loséta básica:
(que también son alturas, bisectrices y medianas), cada uno de los seis triángulos rectángulos formados es la base para la loséta básica:
- Para construir el motivo mínimo nos quedamos con el triángulo rectángulo y trazamos la bisectriz ![]() del ángulo recto que nos proporcionará el vértice del cuadrado interior. Trazamos paralelas
del ángulo recto que nos proporcionará el vértice del cuadrado interior. Trazamos paralelas![]() a los lados por el punto anterior, hallamos las intersecciones
a los lados por el punto anterior, hallamos las intersecciones![]() con los lados y coloreamos los dos triángulos y el cuadrado de los colores elegidos:
con los lados y coloreamos los dos triángulos y el cuadrado de los colores elegidos:
- Este es el motivo mínimo al que vamos a usar las isometría para obtener la celda unidad:
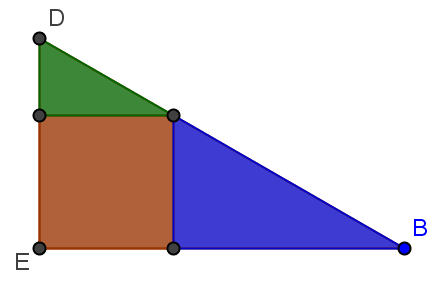
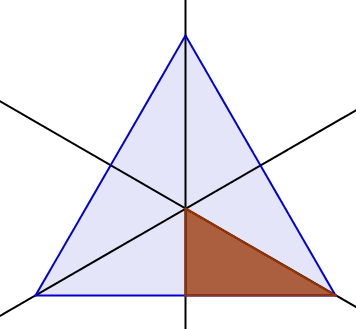
- Primero reflejamos ![]() la figura con respecto de la hipotenusa para obtener la tercera parte del triángulo equilátero, después giramos
la figura con respecto de la hipotenusa para obtener la tercera parte del triángulo equilátero, después giramos ![]() la figura obtenida 120º y 240º respecto del vértice B y tenemos el triángulo equilátero:
la figura obtenida 120º y 240º respecto del vértice B y tenemos el triángulo equilátero:
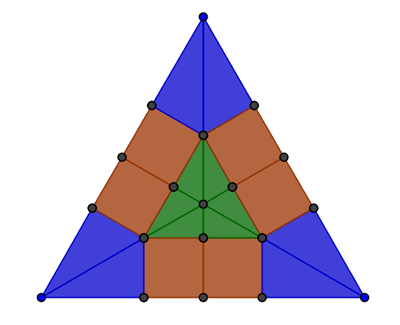
-Girando 60º o reflejando respecto a uno de los lados tenemos la celda unidad que por traslaciones ![]() respecto de los vectores que forman sus lados nos genera el mosaico:
respecto de los vectores que forman sus lados nos genera el mosaico:
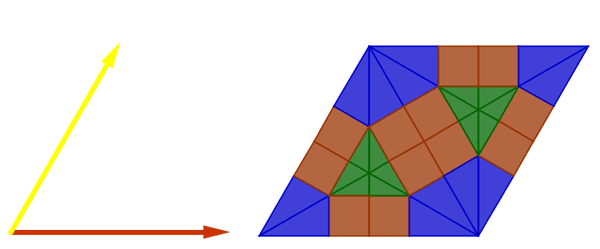
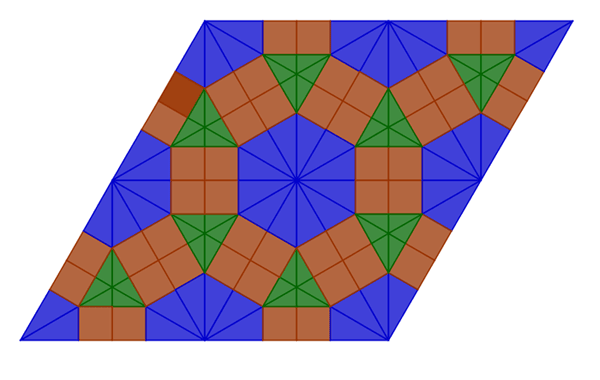
Ahora te toca a ti, dibuja los siete restantes mosaicos semirregulares, que ves a continuación, los guardas y los imprimes con tu nombre.
En esta página tienes dibujados los 8 mosaicos semirregulares por si tanto movimiento no te permite ver la figura
