Frisos y celosías
En una primera aproximación podemos definir una celosía o friso como un motivo que se repite en una única dirección.
Pero dentro de ese motivo que se repite en una dirección, pueden darse una serie de movimientos o isometrías con la condición de que dejen invariante a la recta que pasa por el centro del motivo o grupo de friso, por lo tanto los únicos movimientos que puede contener son de los tipos siguientes:
- La identidad (este movimiento siempre está en un grupo de simetría) (I).
- Traslaciones en la dirección de la recta centro (Tv, en donde v es el vector de traslación).
- Giros con centro un punto de la recta centro y ángulo 180º (G 180º ).
- La simetría respecto de la recta centro ( Sr).
- Simetrías respecto de rectas perpendiculares a la recta centro (Sp).
- Simetría con deslizamiento con eje la recta centro y deslizamiento en la dirección de dicha recta, o composiciones de los anteriores.
Dada una figura cuyo grupo de simetría es un friso, llamamos vector fundamental al vector no nulo y de norma mínima tal que la traslación (Tv) pertenece al grupo de simetría. Llamamos rectángulo fundamental a cualquier rectángulo que contenga al motivo del friso y uno de cuyos lados coincide con el vector fundamental.
Sólo hay siete grupos de frisos esencialmente distintos, que denotamos por la letra F seguida de un subíndice, que denota el orden de los giros que aparecen, y añadimos un superíndice si el grupo no conserva la orientación (contiene simetrías ).
| G 180º | Conservan la orientación ( sin simetrías) | No conservan la orientación (Sr o Sp) |
| No | F1 | F11,F12, F13 |
| Sí | F2 | F21,F22 |
Primero vamos a describirlos y dar algunos ejemplos, unos generados con el programa Kali y otros animados en Flash, después una clasificación, para terminar con un método que nos permita clasificarlos
Grupo primero (F1)
Está formado sólo por traslaciones (Tv) de vector fundamental v que coincide con uno de los lados del rectángulo fundamental. Giro de orden 1, identidad, por eso ponemos subíndice 1. Como conserva la orientación (no tiene reflexiones), no ponemos superíndice.
Ahora practica este tipo de celosía en esta página.
Grupo segundo(F2)
Contiene traslaciones (Tv) y giros de 180º (G180º), de orden2, con centros en la recta central y separados la mitad de la longitud del lado del rectángulo fundamental.

Ahora practica este tipo de simetría en esta página.
Grupo tercero (F11)
Se da una simetría respecto de la recta que es el centro de la celosía ( Sr) y una traslación de vector v (Tv).

Ahora practica este tipo de simetría en esta página.
Grupo cuarto (F12)
Una simetría de eje vertical (Sp) y traslaciones (Tv).

Ahora practica este tipo de simetría en esta página.
Grupo quinto (F13)
Aquí hay una simetría con deslizamiento, una simetría respecto del eje horizontal y después un desplazamiento (cuyo vector es la suma de uno horizontal, v/2, normalmente y otro vertical, nv, para n = entero).

Ahora practica este tipo de simetría en esta página.
Grupo sexto (F21)
Se añade a F2 una simetría respecto de la la recta central (Sr). Tiene también simetría vertical (Sp) ya un giro de 180º ( G180º)equivale a dos simetrías de ejes perpendiculares y una traslación. El centro de giro esta en la intersección de los ejes de simetría horizontal y vertical.
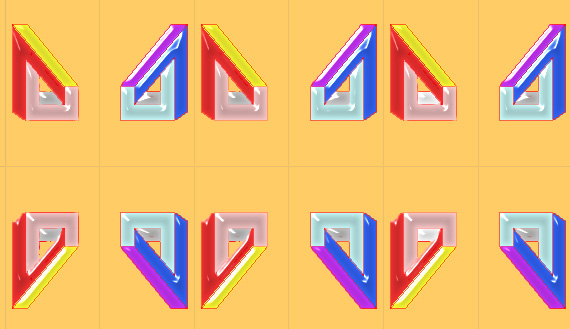
Ahora practica este tipo de simetría en esta página.
Grupo séptimo (F22)
Los ejes de simetría son también perpendiculares (Sp) pero no pasan por el centro de giro como en el caso anterior (sino por el punto medio entre dos centros de giro)(G180º), no hay simetría horizontal.
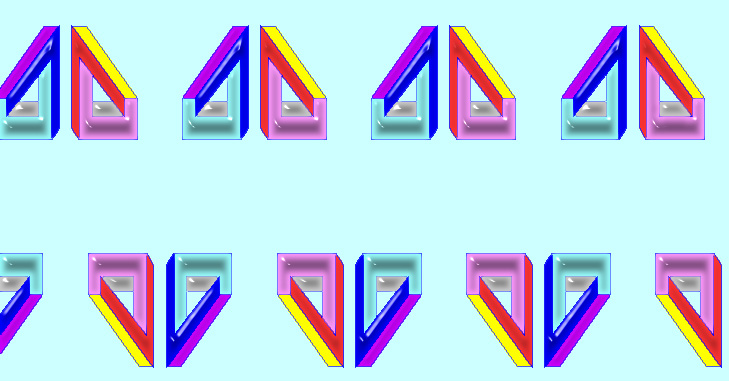
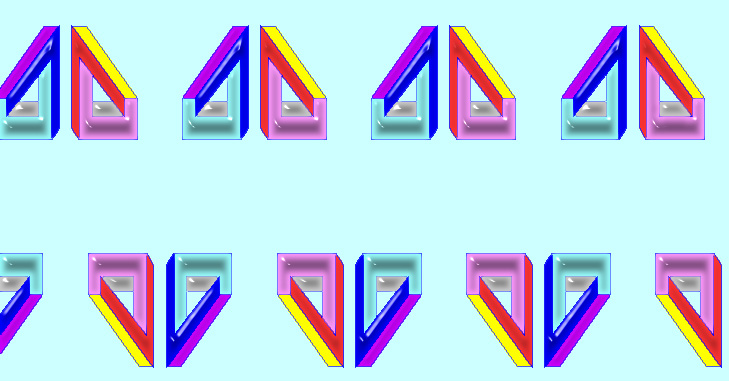
Ahora practica este tipo de simetría en esta página.
Una vez expuesta una somera descripción de cada grupo de frisos, damos una clasificación de sus características :
| Tipo de celosía | Características |
| F1 | No hay giros de orden 2. No hay ejes de simetría ni ejes de simetrías con deslizamiento. |
| F2 | Hay giros de orden 2. No hay ejes de simetría. |
| F11 | No hay giros de orden 2. La recta centro del friso es un eje de simetría. De hecho es el único eje de simetría que hay. |
| F12 | No hay giros de orden 2. La recta centro no es eje de simetría, pero sí hay otros ejes de simetría perpendiculares a la recta centro. |
| F13 | No hay giros de orden 2. No hay ningún eje de simetría. La recta centro es un eje de una simetría con deslizamiento. |
| F21 | Hay giros de orden 2. La recta centro del friso es un eje de simetría. También aparecen ejes de simetría perpendiculares. Todos los centros de orden 2 están en la intersección de dos ejes de simetría. |
| F22 | Hay giros de orden 2. La recta centro del friso no es un eje de simetría, pero hay ejes de simetría perpendiculares a la recta centro. Todos los centros de orden 2 están fuera de los ejes de simetría. |
Un algoritmo (existen otros) para su clasificación podría ser:
| Hay giros de 180º? | ||||||
| SÍ | No | |||||
| ¿ Es eje de simetría la recta central? | ¿ Es eje de simetría la recta central? | |||||
| Sí | NO | Sí | No | |||
| F21 | ¿ Hay otros ejes de simetría ? | F11 | ¿ Hay otros ejes de simetría ? | |||
| Sí | No | Sí | No | |||
| F22 | F2 | F12 | ¿ Hay simetría con deslizamiento? | |||
| Sí | No | |||||
| F13 | F1 | |||||
Después de esta pequeña introducción teórica, pasemos a la práctica:
1) Utilizando el programa Geogebra y partiendo de un motivo semejante a la figura, dibuja un ejemplo de cada uno de los grupos de celosías y guardas los archivos en tu carpeta de clase.

2) Pulsando sobre cada figura tienes algunos ejemplos de mosaicos que pueden formarse, lo que te pedimos es que dibujes, para que veas la diferencia, utilizando Geogebra, al menos una celosía, con cada uno de las figuras siguientes: