Isometría analítica
Ahora, después de hacer un poco de geometría sintética, vamos a estudiar, someramente, las isometrías con respecto a unos ejes de coordenadas (los ejes cartesianos del plano) o sea vamos a hacer geometría analítica con las isometrías.
Traslaciones
Se llama traslación de vector v(vx, vy) a la isometría que transforma cada punto P del plano en el punto P' tal que v =
. Con respecto del origen de coordenadas la ecuación de una traslación, en foma vectorial es r'= r + v, en donde r es el vector de posición del punto P respecto de los ejes, r' es el vector de posición del punto P' y v es el vector de la traslación que aplicamos:
Si cambiamos, moviendo los puntos, el origen, extremo o ambos, cambiamos el vector de traslación y por tanto el punto trasladado P'. Moviendo el deslizador podemos ver la traslación animada.
Las ecuaciones de la traslación son: 
Ejemplo
Sea la traslación definida por el vector v(3, -2). Hallar:
1) El trasladado del punto A(1,6).
2) El trasladado del origen.
3) La recta trasladada de r: y = x + 3.
4) La recta trasladad de s:y = 2x - 1.
---ooo0ooo---
Las ecuaciones de la traslación son: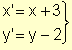 
1) Las coordenadas de punto transformado de A son: A' (x', y') = (1,6) + (3, -2) = A'(4, 4).
2) Las cordenadas del tranformado del origen son O' (3, -2) que coinciden con las componentes del vector de traslación v.
3) Para hallar la recta trasladada, despejamos x e y de las ecuaciones de traslación (x = x' - 3 e y = y' + 2) y las sustituimos en la recta r , y' + 2 = x' - 3 + 3, trasponiendo tenemos la ecuación de la recta trasladada y' = x' - 2, que es una recta paralea a r.
4) Ahora vamos a seguir otro procedimento. Hallamos un punto de la recta dada s, P(0,-1) por ejemplo, calculamos el transformado de P, P' (3,-3), y, como la recta transformada mediante la traslación de vector v será paralela a la recta s, tendrá de ecuación y' = 2x' + n', si sustituimos el punto que conocemos obtenemos -3 = 2·3 + n', luego despejando,n' = -9 y la recta pedida tiene por ecuación: y' = 2x' -9.
Vamos a usar Geogebra para dibujar y comprobar el ejercicio:
Afortunadamente, como ya sabemos, Geogebra nos proporciona una herramienta para transladar objetos [Translada objeto acorde vector] 
y una orden o comando (Translada[objeto,vector ]) que hacen el trabajo duro por nosotros.
Practica con los ejercicios que se te proponen en esta página.
Giros
Se llama giro de centro C y ángulo α, en sentido antihorario, a la isometría que transforma cada punto P en el punto P', tal que d(C,P') = d(C,P) y α = ángulo PCP'. Para simplificar vamos a comenzar por tomar como centro de giro C el origen de de coordenadas O.
El punto P' (x', y') es el transformado de P(x, y) el ángulo α respecto del origen O y también los vectores unitarios i' (cos α, sen α) y j'(-sen α, cos α).
Como el vector OP' = x i' + y j', si sustituimos los vectores unitarios i' y j' tenemos OP' = x(cos α, sen α) + y(-sen α, cos α) = (xcos α - ysen α, xsen α + y cos α)= (x', y'), luego las ecuaciones de un giro el ángulo a respecto del origen son:
que podemos poner en forma matricial :
En Geogebra disponemos de la herramienta [Rota objeto en torno a punto el ángulo indicado] 
y el comando (Rota[objeto,ángulo,centro de rotación]).
Ejemplo
El transformado del punto P(4, 2) respecto del origen y ángulo α = 30º
---ooo0ooo---
El nuevo punto tine las coordenadas:
es
decir P' (2,46, 3,73).
Ejemplo
El transformado del punto P(4, 2) respecto del origen y ángulo α = 30º
---ooo0ooo---
Lo comprobamos en Geogebra:
Para girar una recta tenemos que expresar las coordenadas de la recta r' (x', y') girada respecto del origen en función de las de la recta r original para ello hemos de despejar de la ecuación matricial:
Ejemplo
Halla la recta girada un ángulo de 45º respecto del orígen de 5x-3y = 8.
---ooo0ooo---
La matriz de cambio es 
si sustituimos tenemos 5(x'cos45º + y' sen45º) - 3(-x'sen 45º + y' cos45º) = 8; la ecuación de la recta girada es pues 5,66x' - 1,42y' = 8.
Si el centro de giro es un punto cualquiera C(a, b) distinto del origen, se reduce al caso de un giro de centro el origen, trasladando los ejes a C, lo que hacemos poniendo (x - a) em lugar de x, (x' -a) en lugar de x', (y' - b) en lugar de y' y (y -b) en lugar de y: quedando las ecuaciones de transformación:
y en forma matricial: 
, si llamamos a las constantes c y d, las ecuaciones del giro quedan:
Observa que (c, d) es el punto transformado del origen, puesto que para (x, y) = (0, 0), resulta (x', y') = (c, d) , es decir el vector OO'.
Ejemplos
1) Hallar el tranformado P' de girar el Punto P(4, 4) un ángulo α = 60º en torno al centro O' (3, 1).
---ooo0ooo---
Aplicamos la ecuación matricial de la transformación:
Por último lo comprobamos realizando la transformación en Geogebra:
---ooo0ooo---
2) Halla el centro del giro definido por 
---ooo0ooo---
Es efectivamente un giro ya que 0,82 + 0,62 = 1 y los signos relativos coinciden con los de las ecuaciones del giro. El centro de giro es un punto invariante, es el punto que se transforma en sí mismo, por tanto será la solución del sistema:
luego el centro de giro es el punto O'(2, 1)
---ooo0ooo---
La teoría y los ejemplos creo que ya son suficentes como para que practiques un poco en esta página.
Simetría axial o reflexión
Se llama simetría axial de eje la recta r, a la tranformación que:
1) Transforma cada punto P, exterior a r en el punto P', tal que la recta r es la mediatriz del segmento PP'.
2) Los puntos del eje los transforma en sí mismos.
Las ecuaciones de una simetría se obtienen fácilmente en algunos casos particulares:
Vamos a obtener las ecuaciones de una simetría respecto de una recta que pasa por el orígen.
El vector OP tiene coordenadas (x, y), lo que equivale a poner: OP = xi + yj
Al hacer la simetría, O, P, i, j, se transforman en O, P', i', j' respectivamente, luego: OP' = xi' + yj'. Sustituyendo i' = (cos2α, sen2α) y j' = (sen2α, -cos2α) tenemos :
OP' = x (cos 2α, sen 2α) + y (sen 2α, -cos 2α) = (x cos2α + y sen2α, xsen2α - y cos2α).
Como OP' = (x', y') resulta, igualando coordenadas:
que son las ecuaciones de la simetría cuyo eje pasa por el origen y forma un ángulo α con el eje OX.
En Geogebra usamos el icono [Refleja objeto en recta]
o el comando (Refleja[ ]).
Ejemplos
(1) Hallar las ecuaciones de la simetría respecto a la recta y = (3)(1/2)/3 x.
---ooo0ooo---
Recordando la definición de pendiente de una recta, será: tgα = 31/2 /3 luego α= 30°, 2α = 60°, como cos 60° = 1/2 y sen 60° =31/2/2 las ecuaciones de esta simetría son:
luego el transformado del punto P (5, 1) sería: 
.
---ooo0ooo---
(2) Hallar las ecuaciones de la simetría respecto a la recta y = (3/4) x.
---ooo0ooo---
Las ecuaciones de la simetría son de la forma: 
con a =cos2α y b = sen2α.
Basta poner que un punto de la recta (distinto del origen) se transforma en sí mismo. Por ejemplo, tomando el punto de la recta (x, y) = (4, 3), ponemos que (x', y') también es (4, 3): 
.
Resolviendo este sistema, resulta a = 7/25 = 0,28, b = 24/25 = 0,96.
Por tanto, las ecuaciones de la simetría perdida son:
---ooo0ooo---
Las ecuaciones de una simetría respecto a un eje que no pasa por el origen, se obtienen trasladando el origen a un punto del eje, como se hace en el siguiente ejemplo.
(3) Hallar las ecuaciones de la simetría respecto ala recta y = 3/4 x + 5.
---ooo0ooo---
Trasladando los ejes al punto (0, 5), el problema queda reducido al caso del 3 eje y = 3/4 x, cuyas ecuaciones vimos en el ejemplo anterior, que eran:
Trasladar los ejes al punto (0, 5), se hace: a) dejando x, x' igual, b) cambiando y e y' por y - 5 e y'- 5.
Luego, la ecuación pedida es: 
y haciendo operaciones, resulta: 
Compruébese que el punto (-4,8; 6,4) es el transformado del origen, es decir, que el eje de simetría es la mediatriz de los puntos (0, 0) y (-4,8; 6,4). Esta observación nos sugiere otro método para hallar las ecuaciones anteriores: calcular el simétrico del origen respecto a la recta dada.
---ooo0ooo---
Antes de terminar este apartado: unas prácticas sobre reflexiones en esta página.
SENTIDO EN El PLANO. MOVIMIENTOS PARES E IMPARES
En el plano se pueden considerar dos sentidos de giro. Se indica uno de ellos mediante dos vectores no paralelos, dados en un cierto orden, o mediante un ángulo orientado. Como es sabido, se conviene en llamar sentido positivo al contrario al de las agujas del reloj.
Consideremos el plano sumergido en el espacio. Si el par ordenado de vectores u, v, indica el sentido positivo, su producto vectorial se dirige "hacia arriba", es decir, la coordenada z del producto vectorial es positiva. Ahora bien:
El sentido del par de vectores no paralelos u, v, es positivo si:
es positivo y negativo en caso contrario.
Obsérvese que el par ordenado i, j, tiene sentido positivo.
Una simetría axial cambia el sentido de todo par ordenado de vectores. Se dice que es un movimiento impar, inverso o negativo. Las traslaciones y los giros, conservan el sentido de todo par ordenado de vectores. Se dice que son movimientos pares, directos o positivos.
El significado intuitivo es que, para realizar una simetría axial, se necesita "sacar" las figuras del plano. Recuérdese que había que dar la vuelta al papel transparente. En cambio, las traslaciones y giros se pueden realizar sin "sacar" las figuras del plano.