Aquellos diseños que poseen un centro o ejes de giro alrededor de los cuales sus elementos constituyentes pueden rotar, pero carecen del resto de las isometrías (traslaciones, simetrías axiales o deslizamientos). Se pueden clasificar en dos clases:
(1) Grupos con centro de giro de orden n (denotados por cn) o rotacionales: Tienen un centro de giro de orden n, girando (en sentido horario o antihorario) n veces 360º/n grados se vuelve al motivo inicial.
(2) Grupos con n ejes de simetría centrales (denotados por dn) o diédricos : El motivo se refleja n veces respecto de n ejes centrales de simetría que forman ángulos de 360º/n grados.
Como a veces es difícil distinguir entre un diseño finito y una unidad traslacional de un friso o un mosaico, el dominio fundamental de este tipo de diseños se representa como un sector circular, uno de cuyos bordes ha de estar en la circunferencia circunscrita, los otros dos bordes pueden ser líneas rectas, curvas o irregulares pero siempre pasando por el centro de giro (O) y siendo una la rotación de la otra (respecto de ese centro O) y de manera que el área del sector dibujado sea 1/n del área del círculo de la circunferencia circunscrita si se trata de grupos rotacionales (cn).
Con ayuda de los programas Tess e Inkscape dibujamos un diseño del grupo c4 con tres dominios fundamentales diferentes que ilustran los dicho más arriba:
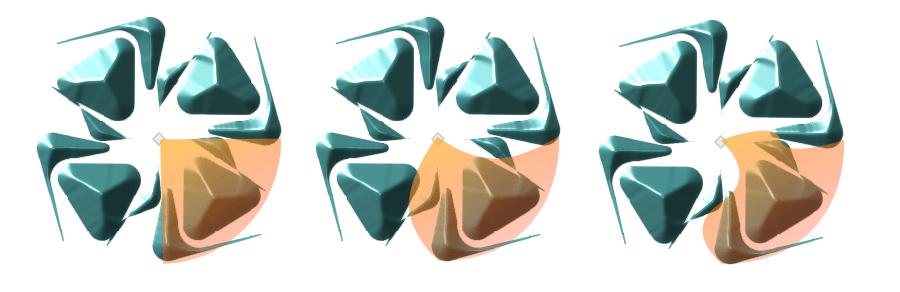
Si se trata de grupos diédricos (dn) también un borde de la loseta básica debe estar en la circunferencia circunscrita pero los otros dos han de ser líneas rectas de centro en O y área 1/2n del área del círculo de la circunferencia circunscrita.
En la imagen siguiente tenemos un diseño finito del grupo d4 (cuatro ejes centrales de simetría, n = 4) en el que la celda base tiene un área de 1/8 del área del círculo, es decir 1/(2·4) del área del círculo que circunscribe el diseño.

Ahora mostramos algunos diseños finitos:









Los diseños anteriores te habrán ayudado a entender este tipo de diseños finitos, antes de seguir practica un poco aquí.
Pero, ¿cómo teselan el plano este tipo de diseños discretos?. Hay diferentes técnicas, por ejemplo aplicando traslaciones (en una o dos direcciones) al diseño original; aquí nos interesa, la técnica que utiliza la composición, es decir aplicar al diseño discreto original otra vez un grupo de los diseños finitos, y después otra composición y otra y así sucesivamente hasta el infinito. Si lo lo hacemos dos veces obtendremos cuatro subgrupos (cn(cN), cn(dN), dn(cN) y dn(dN)) de los cuales las figuras siguientes (creadas con Cabri) pueden servir de ejemplo, en ellas un mismo diseño se somete a una transformación cN y después a otra cn con distinto centro de giro (indicado con º) o bien cn y después dn y las otras dos posibilidades:




















































