Geometría analítica del triángulo
Basándonos en un ejemplo vamos a practicar la geometría analítica del triángulo con Geogebra:
Dado un triángulo de vértices en los puntos de A (-1,5), B(3,-3) y C(8,2). Halla:
1) Las ecuaciones de sus lados.
2) Las ecuaciones de sus medianas y el baricentro.
3) Las ecuaciones de sus alturas y el ortocentro.
4) Las ecuaciones de sus mediatrices, el circuncentro y la ecuación de la circunferencia circunscrita.
5) Las ecuaciones de sus bisectrices, el incentro y la ecuación de la circunferencia inscrita.
6) El área del triángulo y de los círculos inscrito y circunscrito.
Activa los ejes y personaliza la rejilla (botón derecho en la pantalla gráfica).
Dibuja el triángulo pulsando sobre las coordenadas de sus vertices con la herramienta {Polígono} activada.
Ecuaciones de los lados
Ecuación del lado AB
El vector director es: vAB = B – A = (3,-3) - (-1,5) = (4, -8), luego, partiendo de la ecuación de la recta en forma continua, tenemos:
Ecuación explícita del lado AB.
Dibuja ahora la recta que pasa por los vértices A y B mediante la herramienta {Recta por dos puntos} y comprueba que coincide con la calculada.
Ecuación del lado BC.
Vamos a partir ahora, para ir practicando las distintas ecuaciones de la recta, de la ecuación de la recta que pasa por dos puntos:
Ecuación explícita del lado BC.
Dibuja la recta BC y comprueba que coincide con la calculada.
Ecuación del lado AC
Vector director : w = C – A = (8,2) - (-1,5) = (9, -3), luego la ecuación de la recta en forma vectorial es:
(x,y) = (-1,5) + t(9,-3)
Y en paramétricas:
, que pasamos a continua despejando el parámetro e igualando:
Si quitamos denominados, transponemos términos y simplificamos tenemos la ecuación general o implícita : -3x - 3 = 9y – 45 ; 3x + 9y – 42 = 0, x + 3y – 14 = 0 y despejando la y tenemos la forma explícita:
Dibuja la recta AC y comprueba que coincide con la calculada.
Medianas y Baricentro
Primero hallamos las coordenadas de los puntos medios de los tres lados:
1) Coordenadas del punto medio de AB que llamamos M:
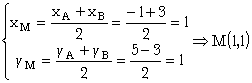
2) Coordenadas del punto medio de BC, N :
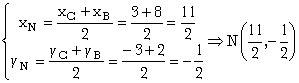
3) Coordenadas del punto medio de CA, P :
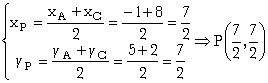
Dibuja los puntos medios de los lados, comprueba que coinciden con los calculados y los etiquetas.
Ahora podemos hallar las medianas:
Mediana, n, que pasa por A( -1,5) y N( 11/2,-1/2)
Dibuja la recta mediana n que pasa por A y N y halla su ecuación comprobando que es la calculada.
Mediana, m, que pasa por C( 8,2) y M( 1,1)
Dibuja la recta mediana m que pasa por C y M y halla su ecuación comprobando que es la calculada.
Mediana, p, que pasa por B( 3,-3) y P( 7/2,7/2)
Dibuja la recta mediana p que pasa por B y P y halla su ecuación comprobando que es la calculada.
El baricentro lo podemos hallar resolviendo el sistema formado por dos medianas, como punto de corte de las medianas:
o bien mediante su fórmula ( menos didáctico, pero más rápido si sólo se ha de hallar G):
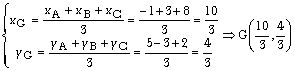
Dibuja el baricentro (punto de corte de las medianas y comprueba sus coordenadas y obtendrás algo similar a:
Alturas y ortocentro
Como las alturas son perpendiculares al lado trazadas desde el vértice opuesto, calculamos primero los vectores directores de cada lado que serán los vectores normales a las alturas:
AB = v = B – A = ( 3,-3) – (-1,5) = (4,-8).
BC = w = C – B = ( 8,2) – (3,-3) = (5,5).
AC = s = C – A = ( 8,2) – (-1,5) = (9,-3).
Altura ⊥ a AB y que pasa por C
es decir, simplificando h1: x – 2y – 4 = 0
Comprobamos que AB ⊥ h1:
Ahora en Geogebra dibuja la recta perpendicular al lado AB que pasa por C, halla su ecuación comprobando que es la calculada.
Altura ⊥ BC y que pasa por A
es decir, simplificando, h2: x + y – 4 = 0
Comprobamos que BC⊥h2:
Ahora lo comprobamos con Geogebra, dibuja la recta perpendicular al lado BC que pasa por A, halla su ecuación comprobando que es la calculada.
Altura ⊥ AC y que pasa por B
es decir, simplificando, h3 : 3x - y – 12 = 0
Comprobamos que AC ⊥ h3:
Ahora lo comprobamos con Geogebra, dibuja la recta perpendicular al lado AC que pasa por B, halla su ecuación comprobando que es la calculada.
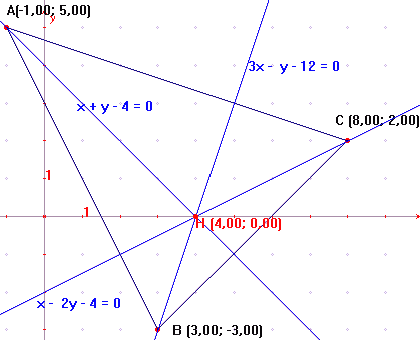
Para calcular el ortocentro resolvemos el sistema formado por dos de las alturas:
Ortocentro H(4, 0).
Ahora lo comprobamos con Geogebra, dibuja la intersección de las alturas, halla sus coordenadas y obtendrás:
Mediatrices, circuncentro y circunferencia circunscrita
Para hallar la ecuación de las mediatrices podemos usar dos procedimientos:
(a) La ecuación de la recta perpendicular al lado en su punto medio, para lo que necesitamos el vector normal (vector del lado) y el punto medio.
(b) Como el lugar geométrico de los puntos que equidistan de los extremos del segmento que forma el lado.
Mediatriz de AB
(a)
que simplificando queda m1 = x – 2y + 1 = 0
(b) A(-1,5), B(3, -3)
Mediatriz de BC
(a)
que simplificando queda m2 = x + y - 5 = 0
Mediatriz de CA
(b) A(-1,5), C(8,2)
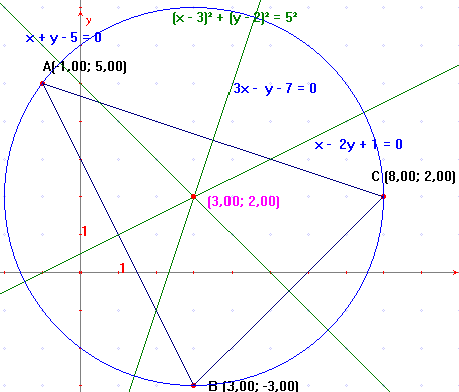
Para hallar el circuncentro resolvemos el sistema formado por dos de las ecuaciones de las mediatrices:
El ortocentro tiene de coordenadas O(3,2).
Ahora lo comprobamos con Geogebra, dibuja las mediatrices, el circuncentro y halla sus ecuaciones y coordenadas.
Para hallar la ecuación de la circunferencia circunscrita necesitamos conocer el circuncentro O(3,2) y el radio que lo calculamos como la distancia del circuncentro a uno de los vértices:
La ecuación de la circunferencia de centro en O(3,2) y radio r = 5 es:
(x –x0)2 + (y -y0)2 = r2, (x – 3)2 + (y – 2)2 = 52 ; x2 –6x + 9 + y2 – 4y + 4 = 25, es decir : x2 + y2 – 6x – 4y –12 = 0.
Con Geogebra, dibuja la circunferencia circunscrita y halla su ecuación:
Bisectrices, incentro y circunferencia inscrita.
Para el cálculo de las ecuaciones de las bisectrices nos basamos en su definición como lugar geométrico:
Bisectriz de un ángulo .- Lugar geométrico de los puntos que equidistan de los lados del ángulo.
Si tomamos un punto P (x, y) genérico de la bisectriz y llamamos r = Ax + By + C = 0 y s = A1x+B1y + C1 = 0, las rectas que forman los lados del ángulo, ha de cumplirse:
Bisectriz en A
Es la recta (b1) que cumple d(P,AB) = d(P,AC), luego como ya tenemos las ecuaciones de las rectas AB y AC, podemos escribir:
, que nos proporciona dos ecuaciones pues hay dos bisectrices la interna y la externa.
Con Geogebra, dibuja la bisectriz interna que pasa por el vértice A, halla su ecuación y decide a cuál de las dos anteriores se corresponde b1.
Bisectriz en B
Es la recta (b2) que cumple d(P,BA) = d(P,BC), luego como ya tenemos las ecuaciones de las rectas AB y BC, podemos escribir:
, que nos proporciona dos ecuaciones pues hay dos bisectrices la interna y la externa.
Con Geogebra, dibuja la bisectriz interna que pasa por el vértice B, halla su ecuación y decide a cuál de las dos anteriores se corresponde b2.
Bisectriz en C
Es la recta (b3) que cumple d(P,CB) = d(P,CA) luego, como ya tenemos las ecuaciones de las rectas CB y AC, podemos escribir:
, que nos proporciona dos ecuaciones pues hay dos bisectrices la interna y la externa.
Con Geogebra, dibuja la bisectriz interna que pasa por el vértice C, halla su ecuación y decide a cuál de las dos anteriores corresponde b3.
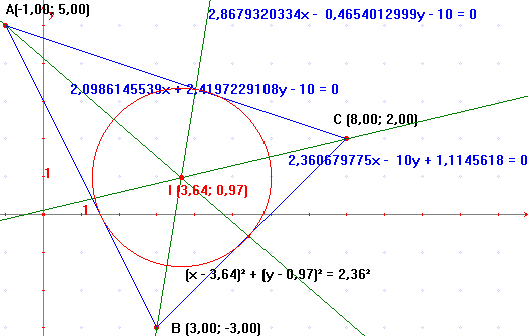
Para calcular el incentro hallamos el punto de corte de dos la bisectrices internas resolviendo el sistema formado por sus ecuaciones:
95,519709 – 20,045905x = 2,5760418 + 5,4561446x ; 25,50205x = 92,943667; x = 3,6445567 y sustituyendo:
, luego es incentro tiene de coordenadas
I(3,6445567, 0,9717974)
El radio de la circunferencia inscrita es:
Y la ecuación de la circunferencia inscrita es ( x – 3,64)2 +(y – 0,97)2 = 2,352.
Con Geogebra, dibuja el incentro, la circunferencia inscrita y halla sus coordenadas y ecuación.
El área del triángulo y el de los círculos, inscrito y circunscrito.
Como el área de un triángulo es A = 
, si tomamos:
Base = b =d(B,C) =
Altura = h = d(A, BC) = 
.
Área del triángulo =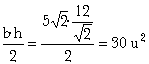 
como puede comprobarse con Geogebra fácilmente.
En cuanto a las áreas de los círculos circunscrito e inscrito como ya conocemos los radios, serían:
AC = 
, que también son fácilmente comprobables con Geogebra.
Ahora practica tú lo aprendido con los triángulos :
(a) A(2,-7), B(4,-1) y C(5, -2).
(b) A(1,7), B(4, 8) y C ( 8, 0).