Fractal de Sierpinski

A partir de un triángulo equilátero y uniendo los puntos medios de sus lados se forma otro triángulo equilátero y en los tres triángulos equiláteros que quedan se repite el proceso:

Para construirlo con Geogebra podemos definir una herramienta que a partir de los tres vértices del triángulo equilátero original construya el triángulo equilátero sombreado de la primera etapa. Después dibujamos los otros tres del segundo paso (que podemos rellenar del mismo o de otro color) y definimos otra macro que, teniendo como objetos iniciales los tres vértices dibuje como objetos finales los cuatro triángulos sombreados hasta el segundo paso, y así sucesivamente.

A partir del triángulo mayor que te quepa en la pantalla de Geogebra, dibuja un triángulo de Sierpinski, hasta el paso 4 o 5 semejante al de la figura:

Te proporciono una nueva herramienta (el último icono) que te permitirá seguir el fractal, se usa pulsando, después de seleccionada, sobre dos vértices (de izquierda a derecha) del triángulo en el que deseas inscribir otro:

Guerda el archivo con el nombre {Sierpinski1}.

Vamos a aprovechar para trabajar un poco las sucesiones numéricas.

Si el área del triángulo inicial es A, es evidente que el triángulo sombreado del primer paso en el triángulo de Sierpinski es la cuarta parte y el área de cada uno de los tres sombreados en el segundo paso es de 1/16 de A y en la tercera etapa cada triángulo sombreado tiene 1/64 de A y así sucesivamente, luego es una progresión geométrica ilimitada de razón ¼, con lo que podemos formar dos sucesiones:

La sucesión de la fracción de áreas sombreadas: 1/4, 1/16, 1/64, ...., (1/4)ⁿ = 1/4ⁿ = 1/2²ⁿ, que es una pregresión geométrica de razón 1/4.

La fracción de la suma de las áreas de los triángulos sombreados hasta el paso n-ésimo que podría expresarse (entre otras) de la forma:

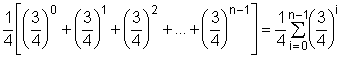
El sentido común nos dice que, si pudiésemos continuar el proceso hasta el infinito, la fracción de área de cada triángulo sombreado tendería anularse y el área sombreado tendería al área del triángulo inicial (A), lo que podría demostrarse a partir de la fórmula de la suma de las progresiones geométricas ilimitadas, siendo la razón r = (3/4):

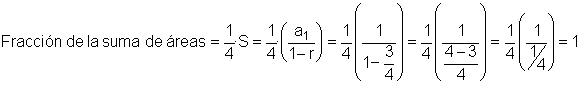
¿Serías capaz de analizar de forma semejante lo que sucedería con los perímetros?. Inténtalo y lo entregas en una hoja titulada: Suma de los perímetros del fractal de Sierpinski.

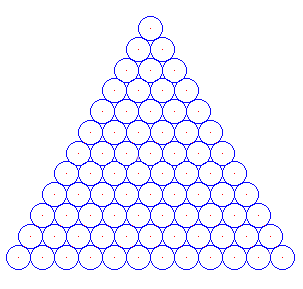
Construye un triángulo de circunferencias como el de la figura siguiente hasta que la base tenga 20 (a medida que las vayas añadiendo puedes ir diminuyendo el radio). Piensa en una macro que te permita obtener un triángulo de circunferencias semejante al siguiente:

Si recordamos el triángulo de Pascal :

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 10 45 120 210 252 210 120 45 10 1

1 11 55 165 330 462 330 165 55 11 1

y hacemos corresponder a cada círculo su número de manera que le dejamos en blanco si el número es impar y le rellenamos si es par se obtiene:

¡ Qué forman un fractal de Sierpinski!

Estudiemos otro punto de vista: Decimos que un número es par si al dividirlo por 2 da cero de resto, esto en la aritmética modular se expresa como 0(módulo 2) = par, y un número es impar si al dividirlo por 2 obtenemos 1 de resto es decir 1 (módulo 2) = impar. Si los pintamos de distinto color obtenemos:

Nos preguntamos ahora ¿qué sucedería si en el triángulo de Pascal tenemos en cuenta múltiplos de otros números? Experimentemos

En la figura siguiente, realizada con cuadrados en vez de con círculos, por comodidad, hemos coloreado de amarillo los números múltiplos de 3, es decir, si el número del triángulo de Pascal es múltiplo de 3, 0(módulo3), lo coloreamos de amarillo y si no en azul, podemos observar que cambia el motivo pero sigue siendo un fractal sierpinskiniano.

Pero, podemos ir más lejos y usar varios colores para los números que dan restos distintos al dividir por 3, es decir, si obtenemos resto cero, divisible por 3, 0(módulo 3) en color amarillo, si obtenemos resto uno, 1(módulo 3) en color azul y si obtenemos resto dos, 2(módulo 3) en color rojo, con lo que obtenemos el fractal sierpinskiniano siguiente.

Si coloreamos de amarillo los múltiplos de 4, 0(módulo 4), y de azul el resto en el triángulo de Pascal, tenemos el fractal sierpinskiniano siguiente:

y si coloremos 0 (módulo 4) de amarillo, 1 (módulo 4) de azul, 2 (módulo 4) de rojo y 3 (módulo 4) de verde, obtenemos el fractal:

Ahora usamos la misma técnica para los múltiplos de 5 en el triángulo de Pascal:

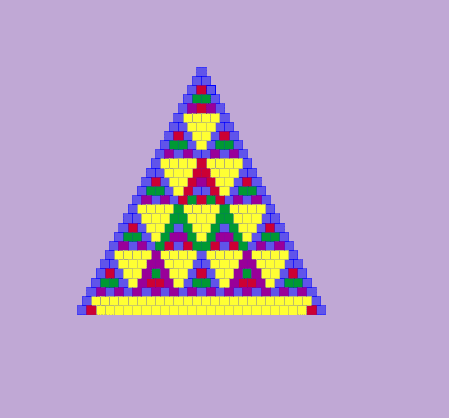
A continuación dibujamos los patrones que se forman al colorear, en el triángulo de Pascal los múltiplos de los 23 primeros números:

Fractal de Sierpinski obtenido al colorear, en el triángulo de Pascal, los numeros pares.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, los múltiplos de 3.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, los múltiplos de 3, animado.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 4.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 5

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, los múltiplos de 5.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 6.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, los múltiplos de 7.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 8.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 9.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 10.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 11.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 12.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 13.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 14.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 15.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 16.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 17.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 18.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 19.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 20.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 21.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 22.

Patrón de Sierpinski obtenido al colorear, en el triángulo de Pascal, múltiplos de 23.

Observa la evolución de los patrones formados con los números primos (la más evidente), los múltiplos de 2, los de 3, los de 5, etc.

Además de colorear los distintos restos con colores diferentes, como hemos hecho hasta mod(5), o preguntarnos qué pasaría con divisores superiores, (como 1000 o 1001), podemos preguntarnos ¿ y si cambiamos la regla de construcción del triángulo de Pascal?, si en vez de sumar los dos números que están por encima, los restamos es decir a_ij = a_(i-1)j(j-1) - a_(i-1)j, pues a ello: