Bisectrices

Bisectriz de un ángulo es la recta que lo divide en dos ángulos iguales, lo bisecta.

Creo recordar que fue en primaria cuando, el maestro nos dijo que para "trazar" las bisectrices de un ángulo en papel había que doblarlo haciendo coincidir los lados que lo forman, ese es el procedimiento que intento reproducir en la animación siguiente para trazar las bisectrices de un triángulo de papel:

Aunque parezca anecdótico la animación anterior tiene más geometría de lo que parece, ¿te atreverías a hacer algo semenjante?.

Pero sigamos con el tema que nos preocupa y ocupa:

¤ Abre un archivo nuevo en Geogebra e introduce un deslizador angular a.

¤ Dibuja una recta r que pase por dos puntos (el inicial A).

¤ Rota la recta r en torno al punto A el ángulo dado por el deslizador angular a, mediante la herramienta [Rota objeto en torno a punto el ángulo indicado] y obtienes el otro lado del ángulo, recta s, cuya bisectriz queremos dibujar.

¤ Marca el ángulo comprendido entre las dos rectas.

¤ Dibuja una circunferencia de centro A y marca los puntos de intersección con ambas rectas como B y C.

¤ Halla el punto medio del segmento BC y llámalo M, activa el trazo de este punto.

¤ La bisectriz del ángulo formado por las rectas r y s es la recta que pasa por los puntos A y M. Compruébalo marcando los ángulos.

¤ Observa lo que ocurre si modificas, variando el deslizador angular, la amplitud del ángulo y contesta al siguiente cuestionario.

Guarda el archivo y envíalo por correo o súbelo a Drive

Contesta a las preguntas del Cuestionario Nº 8.

En las imágenes siguientes hacemos girar las dos rectas que forman los ángulos (cuanto más despacio mejor se dibuja, moviendo el deslizador largo de color morado) y activamos el trazado del punto M, puedes variar la velocidad de giro (cambiando el ángulo del deslizador angular de su color) y observar cómo el punto M va dibujando unas curvas especiales (que concerás si sigues estudiando matemáticas). En la primera animación las dos rectas giran el mismo sentido y en la segunda giran en sentido opuesto. El punto B modifica el radio de la circunferencia y la las flechas de sentido contrario limpian el dibujo y vuelven a la situación inicial.

Otra definición de bisectriz, ahora como lugar geométrico:

Bisectriz de un ángulo es el lugar geométrico de los puntos que equidistan de los lados del ángulo.

Basándote en esta definición puedes trazar, en Geogebra, la bisectriz de un ángulo con el procedimiento:

x En otro archivo dibuja otras rectas t y s que pasen por D.

x Traza una circunferencia con centro en D y obtén los puntos de intersección con las rectas anteriores que llamamos E y F.

x Traza otra circunferencia con centro en E y que pase por F.

x Traza otra circunferencia con centro en F y que pase por E.

x Traza la recta (b) que pasa por los puntos de intersección de ambas circunferencias G y H ( que también pasará por el vértice D del ángulo ) y esa el la bisectriz del ángulo formado por t y s con vértice en D.

Comprobémoslo:

- Elige un punto P de la bisectriz b y mide la distancia desde P a los lados t y s y comprueba que es la misma.

- Si seleccionas el punto con el puntero y los desplazas por la bisectriz comprobarás como las medidas van cambiando pero permanecen iguales entre sí y si modificas la apertura del ángulo moviendo los lados también se conservan las distancias, todos los puntos de la bisectriz ostentan la propiedad de equidistar de los lados del ángulo en que se ha trazado.

- Si activas la traza de los puntos G y H y haces girar cada uno de los lados pulsando y arrastrando E o F, ¿que lugar geométrico forman los puntos G y H?, estudia la figura siguiente pues sobre ella te pregunto en el cuestionario posterior.

Guarda y envía el archivo.

Contesta a las preguntas del Cuestionario Nº 9.

Si realizamos la animación conjunta de los dos lados del ángulo primero en el mismos sentido y después en sentido contrario las trazas de G y H forman las curvas:

Geogebra dispone de una herramienta [Bisectriz] , que nos permite su trazado directamente, sin más que activarla y señalar tres puntos del ángulo, el segundo de los cuales ha de ser el vértice o las dos rectas:

± Dibuja un triángulo acutángulo ABC y etiqueta su vértices.

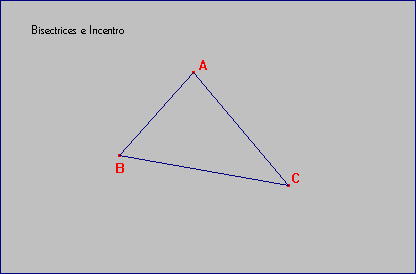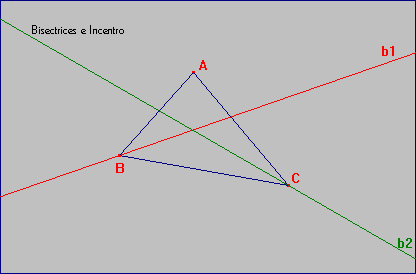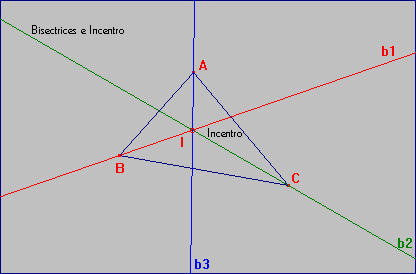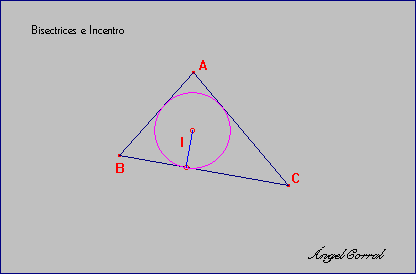
± Activa la herramienta [Bisectriz] y traza las tres bisectrices de sus ángulos (b1, b2, b3).

± El punto intersección de las tres bisectrices (I) equidista de los lados del triángulo y, por tanto, se puede trazar una circunferencia con centro en ese punto y que sea tangente interior a los tres lados, es decir se inscribe en el triángulo, por eso se le llama Incentro.

± Traza un perpendicular desde el incentro a cualquiera de los tres lados del triángulo y llama a la intersección P y traza la circunferencia con centro el incentro y que pasa por P, es la circunferencia inscrita.

± Mide las distancias del incentro a cada lado, selecciona uno de los vértices del triángulo, desplázalo y observa como se modifican las medidas realizadas y que la circunferencia siempre es tangente a los tres lados del triángulo.

Contesta a la pregunta del Cuestionario Nº 10.

Mueve los vértices y observa que se conservan las distancias a los lados. 

Guarda este archivo con tu nombre y Bisectrices3 y lo envías por correo a tu profesor o lo descargas en Drive