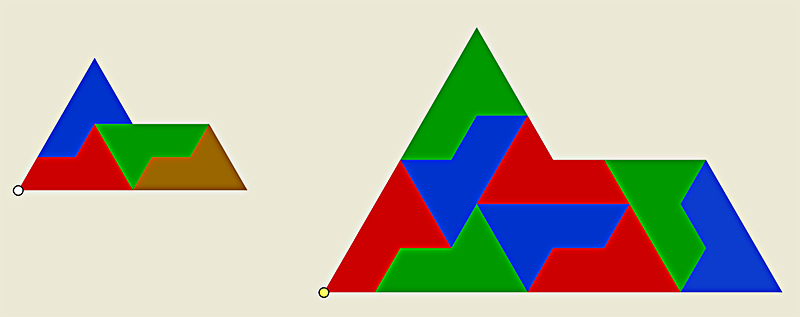
Un reptil pentagonal (sphinx) (Clic sobre la imagen para abrir archivo Geogebra)
Mosaicos por ampliación
Este procedimiento consiste en repetir una loseta base las veces que sea necesario para conseguir otra semejante, de la misma forma pero de mayor tamaño.
En el procedimiento de unir o partir unimos losetas para formar diseños diferentes, en este procedimiento se trata de ampliar la misma loseta básica, al repetir el motivo base.
Es evidente que si partimos de un triángulo equilátero y añadimos otros tres, los cuatro forman otro triángulo equilátero de lado el doble y superficie el cuádruplo del original, con cuatro triángulos grandes se formaría otro el cuádruplo de lado del original, y así sucesivamente, pero no parece tan evidente que el procedimiento se pueda generalizar para cualquier triángulo :
|
|
|
| Ampliación de un triángulo equilátero | Ampliación de un triángulo escaleno |
También es evidente que cuatro cuadrados forman un cuadrado de área el cuádruplo y el doble de lado, y cuatro rectángulos también forman un rectángulo, pero ¿qué cuadriláteros se pueden ampliar?, ¿con qué restricciones ?.
|
|
|
| Ampliación de rombos | Ampliación de un trapecio formado por 3 triángulos equiláteros |
El término RepTiles ( Replicating Tiles) fue acuñado por Solomon W. Golomb para nominar a estas figuras que teselan el plano formando otras semejantes a ellas. El orden es el mínimo número de piezas que se necesitan para formar la figura semejante de grado superior. El triángulo y los paralelogramos son reptiles de orden 4. El trapecio anterior es uno de los tres reptiles posibles con trapecios (el formado por tres triángulos equiláteros, que dibujamos en la figura anterior, el formado por un cuadrado y su mitad y el formado por un triángulo equilátero y medio).
|
|
|
|
Reptil trapezoidal (formado por un cuadrado y su mitad). El de 2º grado tiene orden 4 y el de tercer grado orden 9. |
Reptil trapezoidal (formado por un triángulo equilátero y su mitad). El de 2º grado tiene orden 4 y el de tercer grado orden 9. |
Te proponemos que dibujes con Geogebra, además de las anteriores, las siguientes :

Un reptil pentagonal (sphinx) (Clic sobre la imagen para abrir archivo Geogebra)
Los Irreptiles ( irregular tiles) son figuras geométricas que, con un número finito de copias similares ( no necesariamente iguales), forman una figura semejante a la original. Fueron definidos y propuestos por vez primera por Karl Scherer y es un campo de estudio aún abierto. Todos los reptiles son irreptiles, pero no todos los irreptiles son reptiles.
Los más sencillos son los formados por polígonos en forma de L . En el siguiente, la L está formada por tres cuadrados y es de orden 6 ( 5 piezas originales y una L de lado el doble que la original ):
Irreptil de orden 6, en forma de L
Ahora dos irreptiles basados en el trapecio, el primero de orden 3 y cuyo trapecio base se forma con un cuadrado y medio, también el trapecio mayor se forma igual, pero el lado del cuadrado es la diagonal del primer cuadrado y el segundo irreptil, de orden 5 cuyo trapecio base se forma con dos cuadrados y medio, otro con la diagonal del primer cuadrado y un tercero con dos cuadrados de lado el doble del original :
|
|
|
|
Irreptil trapezoidal de orden 3 |
Irreptil trapezoidal de orden 5 |
El irreptil "cometa" puede obtenerse a partir del triángulo equilátero y es de orden 5 :
Y, pora terminar esta pequeña muestra, un irreptil a base de triminós:
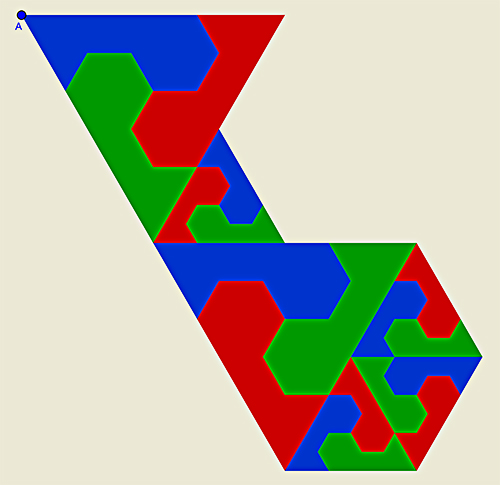
Un irreptil con triminós (Clic sobre la imagen para abrir archivo Geogebra)